Lý sự pclouds

Mèn, đọc tin Mexico và Hàn Quốc dzui dã man. Tội nghiệp Brazil, không có cơ hội rửa hận với Đức.

C++11 is praised for modernizing C++ and all but there are still problems somehow got through and only fixed up in C++14 (which is basically c++11 version "1.1" after the traditionally initial 1.0 buggy release). One of those is this.

Aggregation initialization in C++11 does not play well with default member initializer, which is also new in C++11. Default member initializers are quite easy to get and also very convenient to use. We can write this

#include <iostream>

struct Abc
{
	int a = 1;
	int b = 2;
};

int main(int ac, const char **av)
{
	Abc abc;

	std::cout << abc.a << ", " << abc.b << std::endl;
	return 0;
}

instead of

#include <iostream>

struct Abc
{
	Abc() : a(1), b(2) {}

	int a;
	int b;
};

int main(int ac, const char **av)
{
	Abc abc;

	std::cout << abc.a << ", " << abc.b << std::endl;
	return 0;
}

When there are lots of member variables to initialize, this greatly shortens constructors and improves readability.

Aggregation initialization is actually from C, or originated there.

struct Abc
{
	int a;
	int b;
};

Abc abc = { 3, 4 };

But if any member has default initializer, C++11 does not allow it any more (look for "no default member initializers" in the above link), with a very (also typically) mysterious error

abc.c: In function 'int main(int, const char**)':
abc.c:11:19: error: could not convert '{3, 4}' from '<brace-enclosed initializer list>' to 'Abc'
  Abc abc = { 3, 4 };
               ^

If compiled with C++14 instead, everything is fine.

It took an hour or so to figure this thing out. Moral of the story? Who am I kidding, C++ was and still is a monster language. C++ masters should probably be considered a rare breed.

みそ汁を食べて日本語を勉強する

Xài tmux's last-pane có một cái bực mình. Viết cái patch gần năm rưỡi mà ... lười đẩy lên upstream. Rốt cuộc cũng phấn đấu cho nó vào tmux.git. Coi như năm nay ít ra cũng mần được gì đó.

Next time listen to your soul and avoid "trying something new", stick to Limoncello or at least something stronger.

On the same token, didn't foresee running out of Scott :( Lession learned. Always re-stock alcolhol when any of those run low.

Cái sự ám ảnh FFT mấy bữa nay với video clip về matlab demonstration (ehèm, octave demonstration) dẫn đến cái "lý thuyết" này.

Nhờ trời có Octave, bây giờ có thể "sờ mó" signal processing rồi. Hic.

How in the damn hell did I miss this? GRAAAAHAAHHHHH

Edit: it's also wrong. Signal amplitude should be absolute value of the complex value, not just the I component.

日本語の勉強は難しいよ！ :( :( :(

provided that you know what DFT is (or does) and are not afraid to go through the formula tranformation slowly. Another divide-and-conquer thingy.

Oé oé, đau đầu qué! Mà nó cũng chả có liên quan gì đến công việc. Hic. Toi buổi tối.

Edit: Có liên quan. Xem cái này cho dễ hình dung (ít ra là phần đầu; phần sau của nó là FFT rồi).

Wikipedia có cái hình lẹp lẹp giúp mô tả Fourier transform:

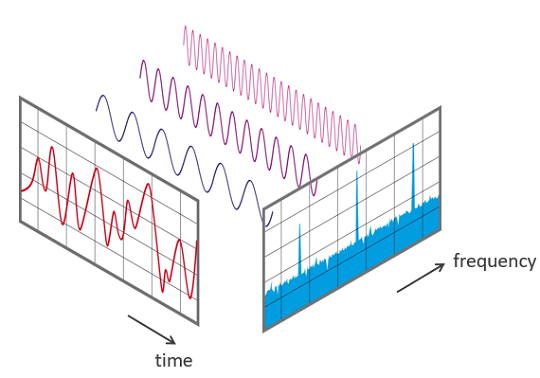
Nói tiếng Việt là, bất kì một mẫu tín hiệu/hàm nào đều là tổng của một tập các tín hiệu cơ bản (sin/cosin). Cái mà người trần mắt thịt nhìn thấy gọi là time domain (biên độ thay đổi theo thời gian). Cái mà không ai nhìn ra là frequency domain: tập hợp tần số của các sóng cơ bản để tạo ra cùng tín hiệu trong time domain. Trong cái hình này, tín hiệu ở time domain là tổ hợp của ba sóng cơ bản (ba trục dọc) trong frequency domain.

Fourier transform chuyển time domain sang frequency domain. Hết phim. Đơn giản thấy ớn luôn. Hiểu được công thức của Fourier transform (chỉ nói về discrete fourier transform) là chuyện hoàn toàn khác:

Bài này có thể giúp hiểu ý tưởng đằng sau cái công thức đáng sợ này. Bỏ qua ba cái phần smoothie nhảm nhí, nhảy thẳng tới time spike và cuối cùng là cách diễn giải công thức:

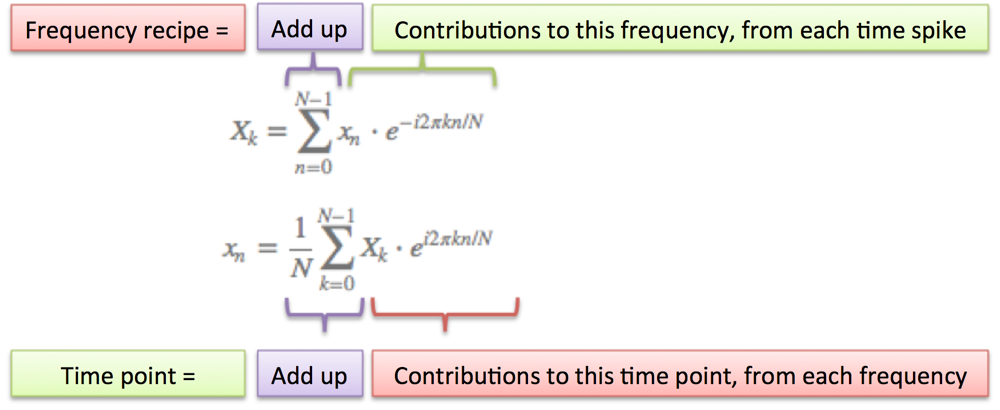
Vài ý chính từ bài viết đó:

• tách tín hiệu ở time domain ra thành từng cột độc lập (gọi là "time spike")
• các tần số tái tạo nên tín hiệu gốc làm được là nhờ chỉnh phase để cho tổng của tất cả tần số là cao nhất ở time spike, nghĩa là tái tạo chính xác giá trị ở time domain ở thời điểm đó, và cộng hết lại thành zero ở những thời điểm khác.
• nguyên cái tín hiệu trong time domain đơn giản là một tập các time spike

Chỉ có một chỗ không rõ là, tại sao giá trị tinh chỉnh cho time spike X+1 không có tác động gì đến time spike X?

Một điểm khác ngoài lề nói thêm về DFT, tại hồi trước không hiểu chỗ này. DFT chuyển từ n-mẫu trong time domain sang n-tần số trong frequenncy domain. DFT không tái tạo chính xác 100% tín hiệu trong time domain (để làm cái đó, có thể phải cần m-tần số, m lớn hơn rất nhiều so với n).

Tuy nhiên, cũng có thể đang hiểu sai về DFT. Bởi vì "tái tạo chính xác" là đang nghĩ về tín hiệu liên tục, không phải rời rạc. Không chừng n-tần số là đủ để tại táo chính xác n-mẫu. Grr...

Tiếp theo, FFT!

Trước khi đi sâu hơn vào sóng vô tuyến và mạng điện thoại di động, bắt đầu từ gốc: sóng điện từ và ăn-ten.

Cái này ai cũng được dạy ở cấp 2 (hay cấp 3?). Vài người nhớ. Nhiều người quên. Thay đổi dòng điện dẫn đến thay đổi ở trường điện từ. Thành ra điện xoay chiều tạo ra sóng điện từ và ngược lại. Một trong những ứng dụng của nguyên tắc này là biến thế: cùng tham số dòng điện nhưng với điện thế cao hơn hoặc thấp hơn. Hai phần của biến thế hoàn toàn tách biệt nhau. Cái chung duy nhất là trường điện từ.

Vậy biến thể có thể "truyền" tham số dòng điện giữa hai mạch điện ở cự ly gần. Nếu coi tham số là thông tin, và đẩy cự ly lên xa rất xa, ta có ăn ten. Đại loại thế. Ăn-ten hoạt động na ná như biến thế. Ít ra trên nguyên tắt nó cũng biến dòng điện xoay chiều thành sóng vô tuyến Cái ăn-ten ở đầu bên kia hấp thụ sóng vô tuyến, tạo ra dòng điện (yếu) cùng tần số như đầu gửi. Nếu tần số là "thông tin", ta có telecommunication.

Trước khi coi các đặc điểm của ăn-ten, cần hiểu cái ăn-ten truyền và nhận trước. Dòng điện xoay chiều về cơ bản là sóng sin/cosin. Ba tham số quan trọng là pha (phase), tần số (frequency) và biên độ (amplitude):

x(t) = amplitude * cos(2 * pi * frequency + phase)

Pha chỉ quan trọng khi so sánh nhiều sóng cơ bản khác nhau. Và bởi vì sóng trên thực tế là một tổ hợp các sóng cơ bản, nó hơi bị quan trọng. Biên độ liên quan đến năng lượng. Tần số cần gì giải thích.

Ở đây cần phải đề cập đến "time domain" và "frequency domain". Cái khác nhau khá đơn giản: time domain thì trục x của độ thì là thời gian, đây là cái dễ dòm dễ hiểu. Frequency domain thì trục x là tần số. Đối với sóng cơ bản, đồ thị trong frequency domain dòm chán ngắt. Bởi vì sóng cơ bản chỉ có một tần số. Đồ thị có đúng một trục dọc ngay vị trí của tần số sóng đó.

Sóng thực tế phức tạp hơn, (Fast) Fourier Transform (FFT) cho phép chuyển từ time domain sang frequency domain. FFT tách "sóng thực tế" thành một tập các sóng cơ bản. Bây giờ nếu dòm đồ thị frequency domain thì sẽ thấy nhiều trục dọc hơn (cao thấp khác nhau tuỳ biên độ). Cái này hình như còn gọi là spectrum analysis. Frequency domain không thể hiện pha được thì phải.

OK quay lại với ăn-ten!

Đặt điểm thứ nhất, cộng hưởng. Tần số gần với tần số cộng hưởng sẽ được "nhận" tốt hơn. Đọc wikipedia hổng hiểu :( Từ từ đọc tiếp.

Đặt điểm thứ nhì, băng thông. Nếu quen với mạng máy tính thì có thể sẽ hiểu nhầm cái này, bởi vì băng thông trong vô tuyến viễn thông là một dãy tần số. Băng thông của ăn-ten cho biết dãy tần số mà ăn-ten có thể gửi và nhận "ngon". Đối với AM thì dĩ nhiên cái này không thành vấn đề lắm bởi vì AM chỉ gửi trên một tần số, tuy nhiên TV hoặc radio sẽ muốn nhần nhiều kênh/tần số khác nhau. Với FM, dĩ nhiên cái này quan trọng bởi vì thậm chí một kênh cũng được gửi trong một dãy tần số.

Thứ ba, gain. Gain cho biết ăn-ten chuyển điện thành sóng tốt cỡ nào khi phát, và sóng thành điện khi nhận.

Phù.. mệt qué.. nghỉ.

Đám làm sóng vô tuyến hoàn toàn không có trí tưởng tượng gì hết. RAT viết tắt của Radio Access Technology. Ai đời lại kiếm chữ viết tắt RAT. RAT là gì? 3G, 4G (LTE) 5G (NR) là đều là RAT. Nói cách khác, RAT là cách truyền tải thông tin qua sóng vô tuyến, ít ra là với điện thoại di động (không chắc WiFi có bi liệt vào hàng RAT không).

LTE (Long Term Evolution) và NR (New Radio) một lần nữa nhấn mạnh sự sáng tạo của 3GPP. Đặt tên kiểu đó, thua.

Làm biếng định viết lăng nhăng về RAT và RAN (Radio Access Network). Ai dè mở nhầm Bảy viên ngọc rồng. Thôi.. mai mốt viết.

Hello Microsoft, goodbye GitHub!